






































pages 466, 467 from "An introduction to the theory of numbers " written by G. H. Hardy and E. M. Wright.
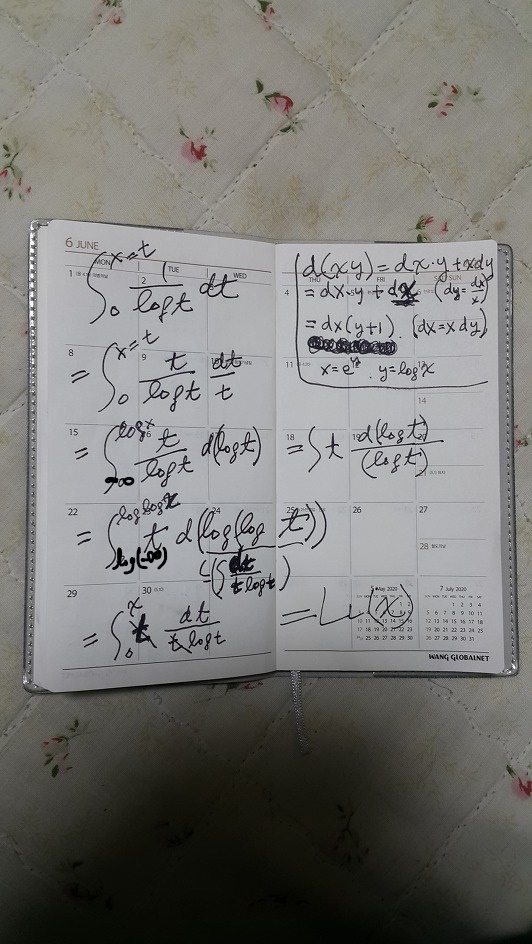
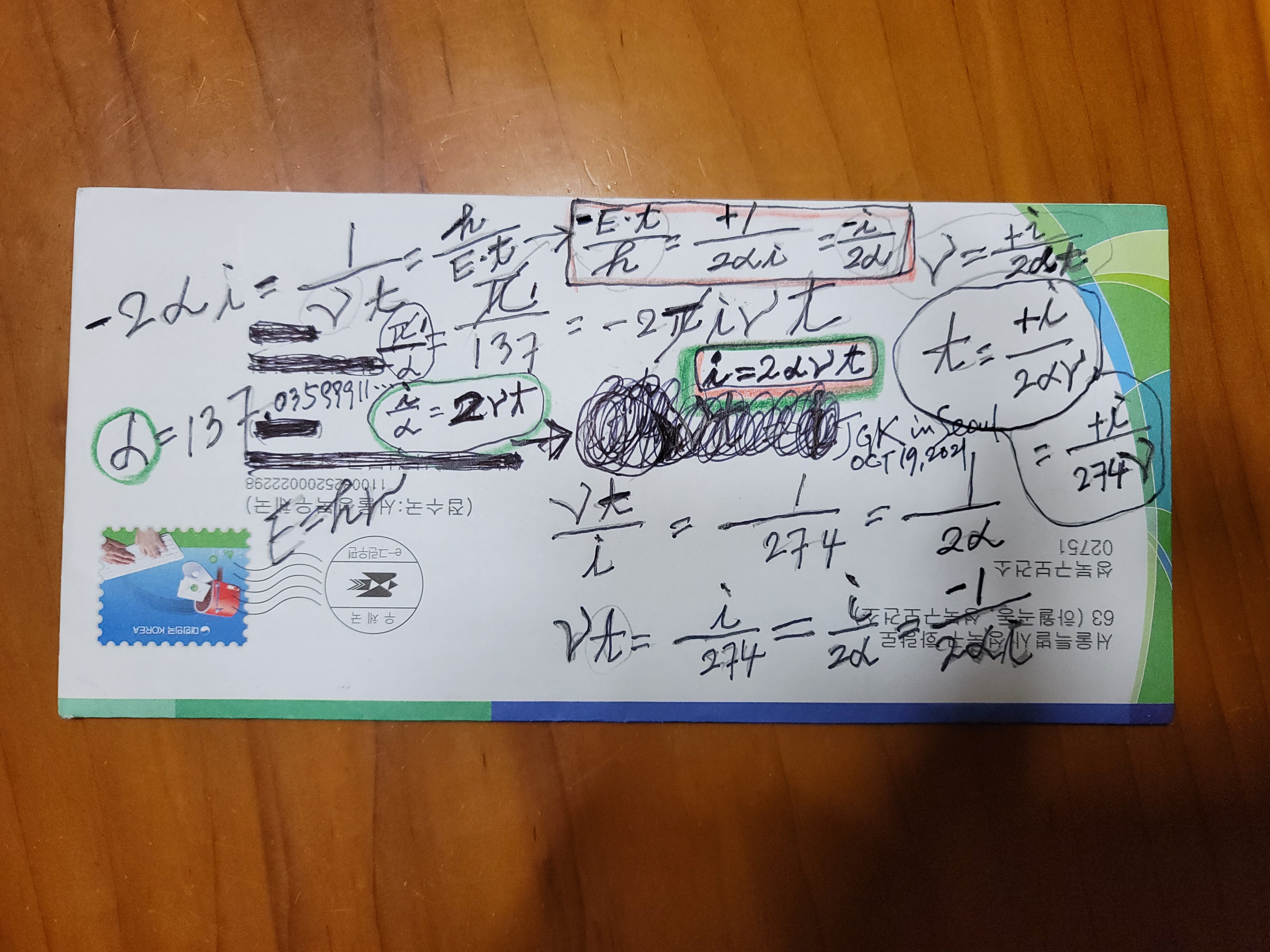
2021. 9. 24. 새로 필산으로 계산 해보다 :







윗사진 1)번 t d (d lnt )부분은 2005년 당시 실력이 모자라 실수. t d ( ln ln t ) 로 수정해야한다. 그림은 대체적으로 옳다.

Quoted from the book " An introduction to the theory of numbers " written by G. H. Hardy and E. M. Wright
page 466.














수학에 취미있는 분들만 읽어주시기 바랍니다. 너무 일상과는 동떨어진 주제이기 때문입니다.
Julian Havil 이란 사람이 쓴 "Gamma" 란 책을 요즘 아주 재미있게 읽고 있다.
내가 아래에서 소수라 표현하고 있는 수는 1 과 자신으로 밖에는 나눌수 없는 소수(Prime Number)
로서 소숫점이하 몇 할때의 소수가 아니다.
지난번글 RH-11 에서 1 +2 +3 .....= - 1/12 이란 예기를 했었는데 그건 거기 썼듯이 라마누잔이
1913 년 G. H. Hardy 에게 편지를 쓰면서 한줄 슬쩍 넣은 부분에 나오는 예기인데 그것에 관한
진실은 리만의 1859년 논문에 그 속 사정이 나와 있다. 리만의 앞뒤로 써서 달랑 3장짜리 논문원본
은 그가 수학교수로 있던 독일 괴팅겐대학에 잘 보관 되어 있는데, 라마누잔이 인도 마드라스에서
캠브리지대 Trinity College의 수학교수 하디에게 보낸 그 편지는 하디가 동료들과 돌려보며 여러
사람 손을 타서 원본은 분실 된걸로 알고있다. 특히 라마누잔의 유고 노트들은 정말 수학계의 보물
들이며, 리만의 논문은 국보급 보물이다. 여담이고, 저 수열의 합이 왜 -1/12 로 나오는가 하는 예기
부터 해볼까 한다.
물론 우리가 쓰는 실수의 세계에선 1+2 +3 ....은 무한대가 정답이다. 그러나 복소함수의 세계로
들어가면 답이 -1/12로 나오는데 보통의 사람들이 좀처럼 이해하기 힘든 소위 함수의 해석적 확장
이란 세계에선 -1/12 이다. (고백컨대 나자신도 왜 그리 되는지 하빌의 책을 읽고 최근 믿게 되었다.)
그러고도 나는 나의 우스꽝스런 나의 졸작 논문을 프린스턴에 보냈었고 거부 당했었다. 그러나,
나에겐 또다른 나의 사색의 세계가 있긴허다. 그래서 졸작이지만 그걸 보내 봤던거구...암튼,
그러면 1+1/2+1/3+...(소위 고등학교서 배운 조화수열의 무한합이다)은 그 세계에선 답이 무엇일까?
그것이야 말로 그 세계에서도 유일한 무한대이다.(소위 리만 제타함수 ζ(s)는 s값 1에서 유일하게
정의할 수 없다. 그점 즉 s=1 이외에서는 제타함수가 복소수 값을 갖는 함수값을 갖는다.)
소위 조화수열의 무한합 (무한대)야 말로 그들 리만, 하디, 라마누잔의 세계에서도 어찌 정의 할
수 없는 유일한 무한대 값이다. 하늘에 뚫린 유일한 구멍이라고나 할까. (하빌의 그 부분 설명을
읽고 오늘 무릅을 쳤다. 그리고 뉘우쳤다. 이런 프로세계의 기초도 모르고 논문을 썼었다니 하고
말이다, 나란 인간 참 주제넘다.).
그리고, 좀 웃긴다. 실수의 개념으로 보면 분명 누가 봐도 1+2+3... > 1+1/2 + 1/3... 이니 말이다.
자 이제 그런 세상이 아닌 리만, 하디,라마누잔의 세계로 가보자. 그리고 그런 세계를 만든이는
오일러이다. 그가 소위 허수 i 라는 걸 만들었기 때문이다. 이놈의 " i "하나 때문에 그런 천지
개벽할 바뀐 세상이 존재 한다니 참 문자의 힘, 심볼의 힘이 무섭다.
세상을 진짜 바꾼이는 리만인데 그 3 장(6쪽)짜리 논문에서 거침없이 방정식들을 뛰어 넘는 전사
리만의 정신세계의 진수를 볼 수 있는데 그는 사진으로 보면 참하게 생겼고 말수가 적은 많이 타인
을수줍어 하는 그런 사람이었다고 한다. 그가 남긴 그 정신세계 때문에 후세들이 엄청난 노력을
경주하고 있는데,
소위 리만가설이 들어가 있는 부분의 그의 말투를 보면 참 평이하다. 아마도 근들이 일직선위에
있지않을까 생각한다(리만가설). 나 자신도 연구해 봤는데 엄밀한 증명에는 실패했다. 뭐 이런식의
몇 마디그의 말이 학계에 불을 질러놓고 그 불이 150 년째 타고 있으며 그걸 증명하겠다고 그리고
증명했다고 나섰다가 모두 실패하고 죽어갔고, 지금도 엄청많은 아니 소위 유명 수학자는 모두 다
암암리에 그걸 시도하고 있다고 나는 생각한다. 왜냐면 수학계의 넘버원 화두이자 인류의 숙원이기
때문이다.
그러나 설사 그게 증명되도 실생활에 도움을 줄 일은 별로 없을거고, 증명되는 순간 거기에 매달린
모든이를 실업자로 만드는 재앙일수도 있겠다. 그러면 사람들이 왜그리 상금까지 걸어가며 난리들
일까? 그건 진짜 어려운 문제이기때문이다.
바로 그거다. 안풀린다는 것. 내보긴 그게 제일의 이유이다. 쉽게 말해서,이게 꽤나 똑똑하다고 자만
내지 자부하는 수학자들의 심기를 심히 자극하기 때문이다. 힐버트는 500 년 후에 혹 환생하면
"친구들. 그간 리만가설이 풀렸나?"하고 질문할 거라고 했듯이 시쳇말로 x 때리는 문제이다. 아마도
그런 문제들과 씨름하고 살다보니 가난하고 고독한 영혼이었던 리만이 40살에 죽었나 보다.
리만논문은 그가 33살적에 독일학술원(Berlin Academy of Sciences) 회원이 된 기념으로 그가
제출한 짧지만 그 누구도 흉내낼 수 없는 걸출한 수학 논문이다.
화제가 자꾸 딴데로 가는데 본론으로 들어가자. 그러면 왜 함수의 정의역이 복소평면인 제타함수
에서 그런 천지개벽이 일어 났을까? 그건 리만이 소위 Contour Integral 을 복소평면에서 하면서
제타 함수가 교묘하게 자이함수로 확장되면서 벌어진 일이다. 그걸 수학자들은 함수의 해석적
확장 *** (Analytic Continuation of Riemann zeta function)이라 한다. 그러면서 새 방식으로 계산해
보니
*** 註 이 글을 혹 읽을 수 있는 미지의 독자에게....
리만 제타함수의 해석적 확장... 딱 12 글자이다. 이게 뭔 요물인지 저도 잘 모르지만 복소해석학( COMPLEX ANALYSIS)이란 꽤나 어려운 수학을 제대로 접해 보지 못한 분 들은 결코 이해 못하는 물건 이란 걸 여기 확실히 부기 해둔다. 글로 써 있다고 다 뜻을 알 수 있는 것 이란 생각은 버리시기 바란다. 본글의 저자인 저도 한 30년째 매달려 본 문제이지만 아직 그 실체를 모르겠다는 걸 여기 밝혀 둔다. 그러니 관심없는 분 들은 말할 것도 없고 어쭙지 않은 생각으로 섣불리 이해하려 덤비는 이가 있다면 인생의 시간을 낭비하게 될 가능성이 농후하므로 이 문제 말고 딴 중요한 문제를 풀며 사시기를 조언 드린다. 리만가설이 약 160년전 세상에 공표되고 나서 그 증명의 도전에 나섰다가 스러져 갔던 수많은 선현들을 생각 할 때 이건 현실적인 진심의 조언이다. 그래도 어딘가에선 그 누군가가 도전에 나설 것 이라는 것도 나는 물론 안다. 2020. 06. 16.
1+2+3...= - 1/12 요, 1+1+1+...= - 1/2 이요, 1^2 +2^2 +3^2....은 0 (이런걸 trivial zero라고 한다 모든
짝수 제곱의 수열합은 0 ) 이요 뭐 이런 식으로 실수세계에선 모두 무한값을 갖는 것 들이 실수 또는
복소수값들로 다소 황당하게 바뀌게 된다. 그러니까, 리만이란 이름의 요지경을 끼고 세상을 보면
세상이 많이 아니 아주 많이 달리 보인다는 예기다.
위에서 유일하게 어찌 정의 해 볼수 없는 값이 1 + 1/2 +1/3 +.......................= 무한대 라고 했다.
그런데 그 합에는 예전에 예기한 오일러 상수 감마(γ) 0.57721.................. 가 포함되어있다.
즉, ∑(1/k)=log(무한대) + 0.57721....(원주율 같이 소숫점 이하 무한히 값이 나오는 걸로 사람들은
믿고있고 그게 유리수인지, 무리수인지 그리고 다항식의 근이 아닌 초월수인지 아직 아무도 모른다.
왜냐하면 수식엔 무한대가 들어가 있는데 무한대는 숫자가 아니다).
수학상식 하나 더, 0 의 0 승은 1 (이건 정의임), 0 의 무한소(ε) 승( 0^ε, ε 는 무한소)은 0,
0의 0승의 0승은 ? ε^ε^ε , x^x^x^x^x 등등은 나도 모른다.
하늘에 뚫린 구멍 1+1/2+1/3... 그리고 0.57721.........그리고 제타함수의 근이 수직선인(1/2)+it
(t는실수)축상에 있다는 리만가설. 나에겐 재미난 주제이다. 리만은 필산으로 6개의 t 값을 구했고
최초의 근은 t=14.1347..이고 그위로 무한히 많은 값이 있다. 마이너스 쪽으로도 대칭적으로 같은
위치에 근이 존재한다. 복소평면상 왜 그 일직선 상에만 근이 존재하는 것일까? 참 신비하다.
인류는 현재 콤퓨터로 수조이상개까지 계속해서 리만제타함수의 근의 존재를 확인중이다.
t 가 0 에서 아주 큰수인 T 구간에서 근의 존재 빈도 (밀도) 는 t 가 커질수록 그 빈도 (밀도) 가
log(t/2 pi) 에 비례하여 높아진다고 리만은 예상했으나 리만가설이 증명안된 상태라 그것은 누구도
확인해 줄 수 없다. ( 밀도를 적분하면 갯수가 나온다는 개념하에서 한말 ).
리만은 논문에서 리만가설의 증명에 대한 예기는 접고, 소수의 분포에 대한 논의를 계속하게 되
는데, 그것이 제타함수의 근들 ( 영어로는 근들을 Zeros 또는 Rhos 라 쓴다) 과
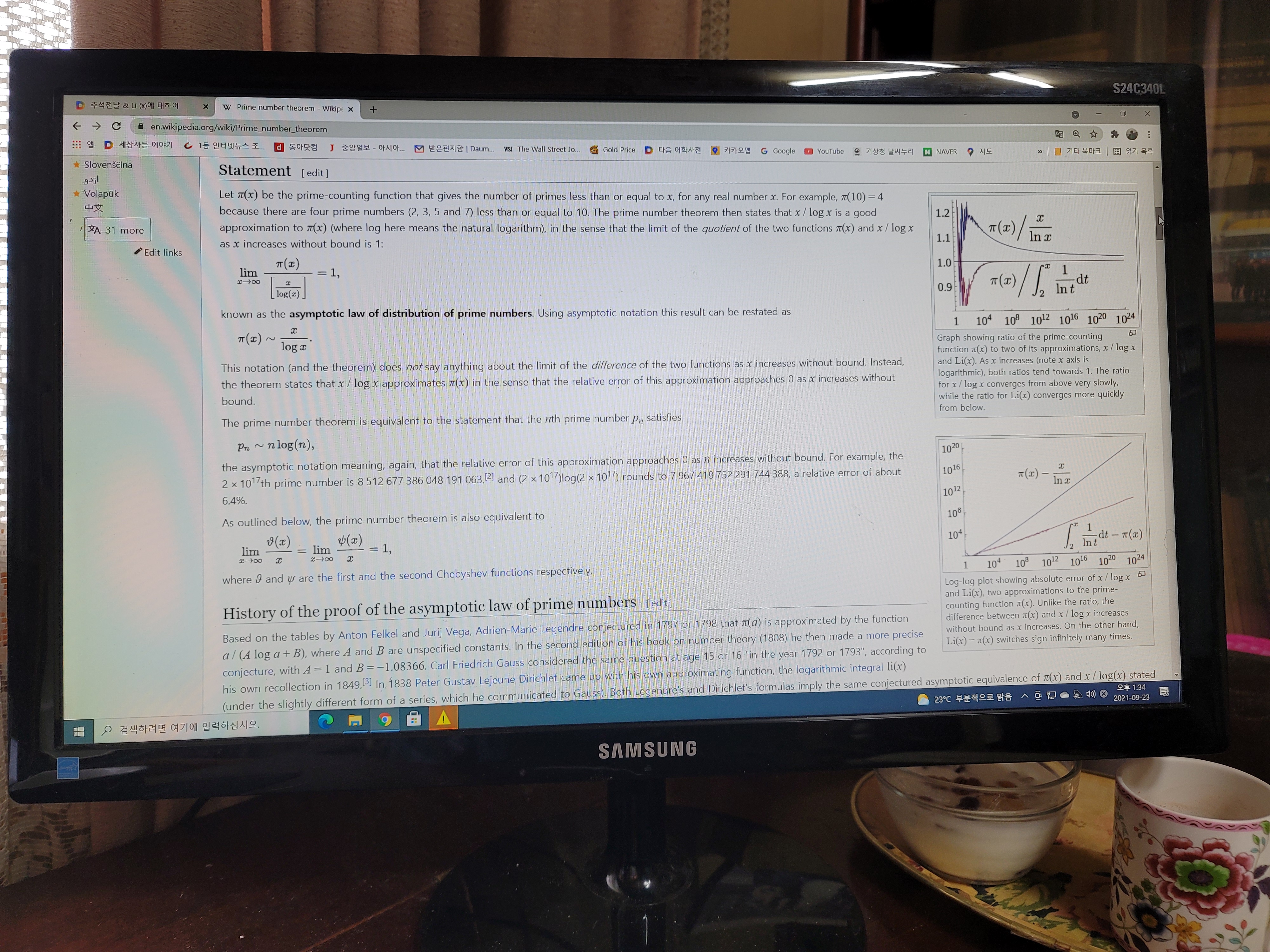
밀접히 연결 되어 있다. Log Integral 이란 적분함수가 있는데
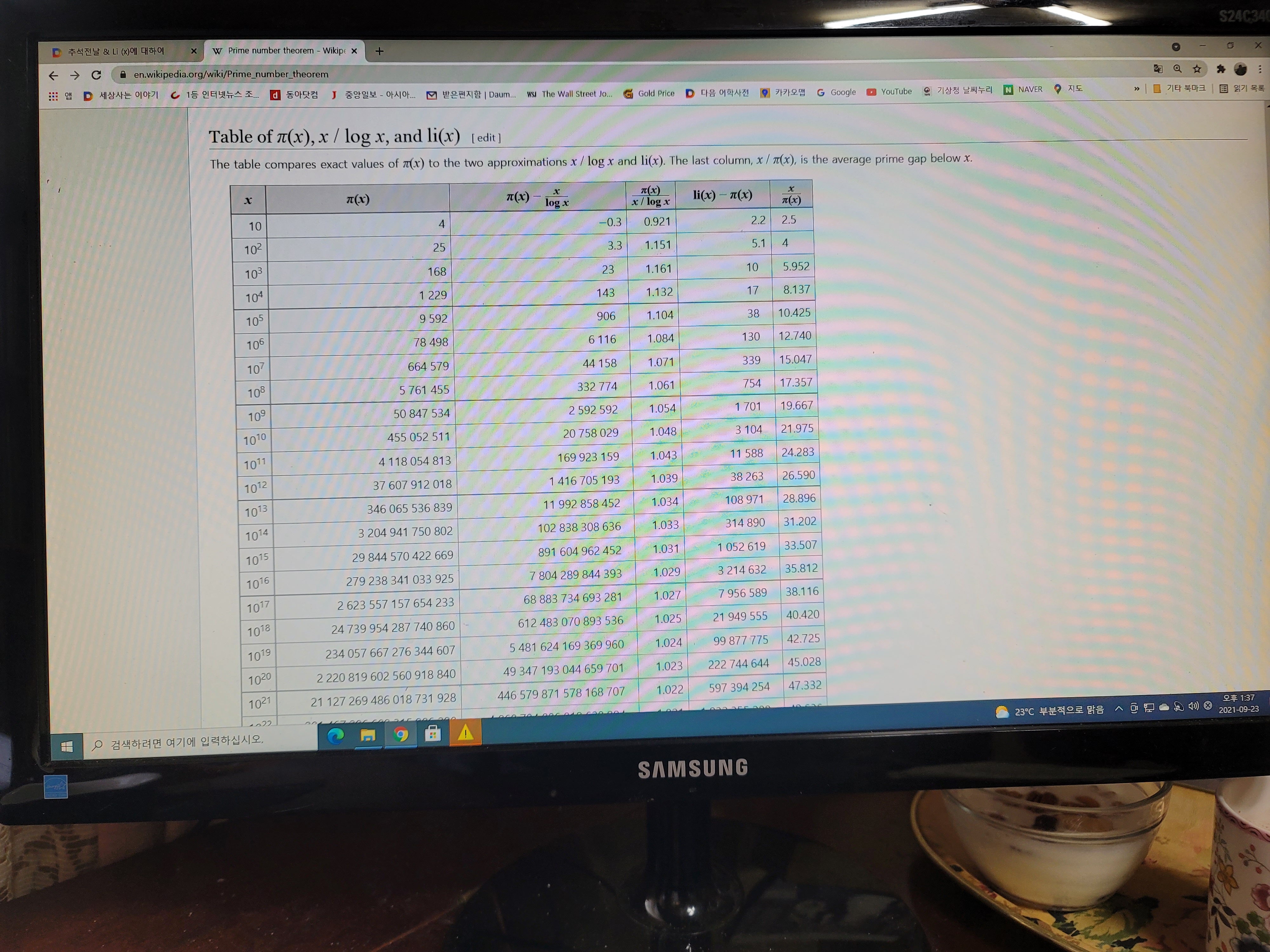
Li(x)=integral ( 0 에서 x) (1/log t )dt 로 정의된다. (한편,가우스의 정의에선 2 에서 x 까지 적분,
거기엔 다른 이유가 있다. 수학/공학을 해서 로그인테그랄이 뭔지 아는 사람은 다 알 것이다.
이것도 x 때리는 적분중하나). 이 적분 값이 "0 에서 x 까지의 소수의 갯수"(이게 사실 리만논문의
제목임, 통상 그 값을 π(x)라 부름 )를 근사치로 잘 반영한다고 알려져 있다. 그리고 그 증명은
지난세기말 Jacques Hadamard 와 Charles de la Valee Poussin 라는 두 불란서 수학자에에
의해 1896년 증명됐다.
(Prime Number Theorem-소수정리: 무한대까지의 소수의 갯수는 lim(x->무한대) ( x/log x) 임) :
Li(x)~π(x) (~는 근사치란뜻, 가우스, 리만 시대의 사람들은 당시 계산력의 한계로 인해
항상 Li(x) 가 π(x)보다 큰걸로 믿고 있었음. 오늘날엔 1.398 X 10^316 에서 그게 최초로 반전되고
그보다 더 큰수들로 갈수록 부등호의 반전이 계속 엎치락 뒷치락 할거라고 알고 있음.
정말로 큰 수의세계로 들어가면 정말 가관임.
10^316 만 해도 엄청 큰수임 물리학에선 10^70 정도의 Scale로세상에서 모든 작은것
(소립자)와 모든 큰것(우주)이 끝이남. 이런 관점에서 볼때 순수수학이며
수학의 꽃이라 불리는 정수론은 신학과 가장 가까운 학문일 수 있음.)
리만은 x/log x 보다 개선된 소수의 갯수를 구하는 근사치 함수를 그 논문서 구해 내는데, 그의
엄청난 정신력과 마스터의 기량이 정말로 돋보이는계산과정이 그 속에 있다.
(지난번에 난 고백 했었다, 나는 리만가설에 관한 논문을 한번 써본 사람이지만 실은 그의 논문
내용은 잘 모른다고... 이젠 그간 공부가 좀 진척되고 쌓여 예전 보단 더 많이 이해 하지만 아직
절반도 이해 하지 못했다. 번역본으로 된 내방에 있는 그의 논문은 빨간줄 투성이로 점철 되어
있다. 하도 돌머리 로 이해 해 보려 노력 하다보니).
실제로 리만이 논문서 제시한 그의 근사식으로 계산해보면 어지간히 큰 수에선 아주 잘 맞는다.
그러나,
그도 옛날사람이라 x=10^316 (10의 316승, Skewes Number 라 불리는 수는 10^10^10^34임)의
세계로 들어가면 그의 근사식도 잘 맞지않는다는 게 오늘날의 콤퓨터의 계산결과로 알려져 있다.
리만이 무식해서 근사식을 제시 했을까?
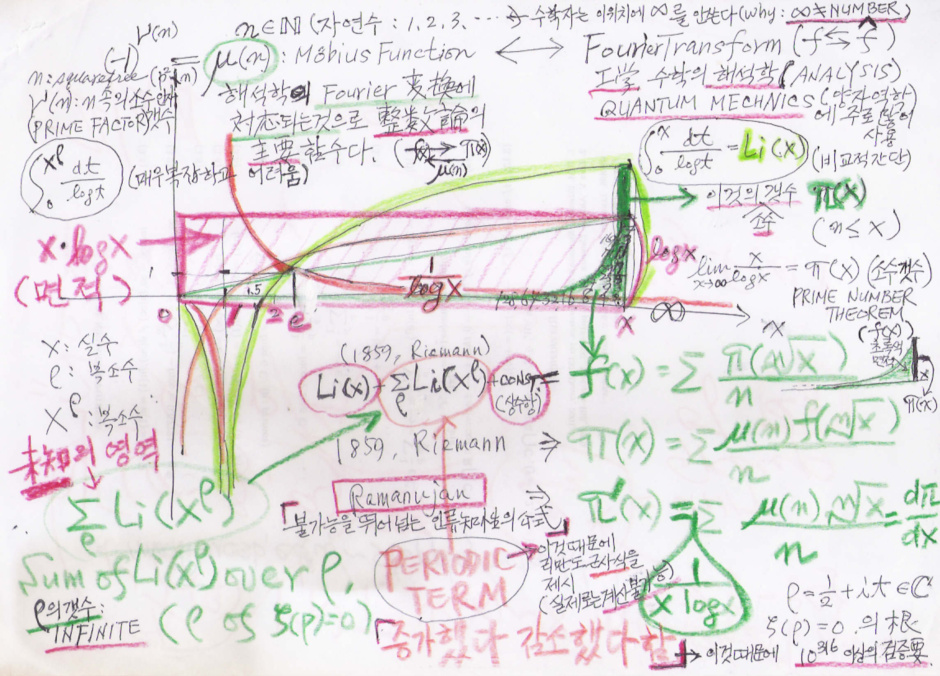
아니다. 그의 논문엔 완벽한 형태의 π(x) 식이 있다. 그런데 π(x)를 유도해 내기 위한 아래의 f(x)
속에는그것의 두번째 항에 소위 값이 늘었다 줄었다하는 학자들이 예기하는 Periodic Term 이
들어가 있는데, 바로 그 항속에 제타함수의 무수한 근( ρ=(1/2) + it )들이 녹아 들어가 있기 때문
이다.
π(x) = Σ_m (-1)^(ν (m)) (1/m) f <x^(1/m)> : Fourier Tranform 의 방법으로 아래의 f(x)에서 유도.
자연수 m에 대해 합산. m은 1 이아닌 어떤제곱(square)의 수로도 나누어지지 않는 수.
ν(m) 는 자연수 m 속에 있는 서로다른 소수인자의 갯수 (모든 자연수는 소수로 인수분해된다),
ν(m) =number of squarefree distinct prime factors of m. (-1)^ν(m)=μ(m)=0, 1, -1.
리만은 여기서 그의 근사식을 제시한다, 왜냐면 위의 식엔 다루기 힘든 제타함수의 무수한
(infinite) 근들이 포함 되어 있기에.
f(x) = Li(x) + Σ_ρ Li(x^ρ) + 상수항 : 이 함수가 Fourier 변환으로 윗식에 들어가 있다.
( 두번째 항이 문제로 무한히 많은 제타함수의 근인 ρ 에 대한 더하기, ρ=(1/2) + i t ).
20 세기 초반 영국의 캠브리지대 수학교수 하디 교수는 제타의 근인 rho들이 일직선에 무수히
존재한다는 걸 1914년 그의 논문 " Sur les zeros de la foncion ζ(z) de Riemann"에서증명했
는데, 그가영국으로 불러 들여 공동연구자로 활동한 33살에 요절한 인도인 라마누잔은 그의 천재
성을 발휘하여 한수위인 놀라운 아래의 공식의 증명을 해냈다.
dπ(x)/dx=(1/ x logx) Σ_(n은 1~∞) μ(n) x^(1/n) /n
(μ(n)은 뫼비우스함수, n은 자연수. μ(1)=1, 기타 μ(n)은 n이 중복되는 소수쌍을 인자로 가지면 0 ,
n이 짝수의 소수인자를 가지면 1, n이 홀수의 소수인자를 가지면 -1 이 되는 함수, 공간반전을 연
상시키는 함수이다, 그걸 뫼비우스 Inversion 이라 부른다 ). (J. Havil's Gamma, p199).
남들은 소수의 갯수의 논의와 그의 극한값을 논할때 라마누잔은 그 변화율에 대한 공식을 내놓고
증명 했던 것이다. 실로 무한대를 마음대로 넘나 들었던 라마누잔이 아니면 못 만들 공식이다.
독실한 기독교인 이었던 리만(40살 요절, 1826-1866), 무신론자였던 G.H. Hardy(70살 사망,1877-
1947), 그리고 비록 가난했으나 인도의 Brahman 계층 출신이었던 라마누잔(33살 요절,1887-1920).
세 사람다 정수론의 걸출한 귀재들이었으나 무한대를 가장 자유자재로 다루기는 아마도 세분중
에서 다신을 믿는 독실한 힌두교신자 라마누잔이 아니었을까 싶다.
그간 좀 쉬었기에, 나의 공부 중간중간에 후일 기억 할 수 있도록 잡문삼아 한번 써봤다.
그건 그렇구, 위에 언급한 세분중 누가 가장 신의 총애를 받고 있을까? Who is His favorate guy
now?그건 아마도,생전에 그분을 믿지 않았던 G.H. Hardy 가 아닐까 싶다. 선생님들두 말 안듣는
놈들을 자기곁에 가까이 두고 괴롭히길 좋아 하지 않던가? 글구, 하디는 70평생 독신이었고, 리만,
라마누잔은 모두 결혼했던 사람들이라 자신도 결혼 같은건 모르는 그 분 께서 보다 더 동료의식을
하디 에게 느끼지 않을까?
하디란 사람 여러모로 내겐 끌리는 데가 많이 있는 인물이라 앞으로 보다 상세히 연구할 예정이다.
To Be Continued.









* 윗 사진의 손가락 표시된 부분이 리만가설이다 : " 아마도 모든 근 (1/2 + i t ) 의 t 값이 실수 일 것이다 (리만가설). 나 자신도 그 증명을 위해
덧없고 헛된 시도들 ( some fleeting futile attempts) 을 해본 후 나의 다음 연구 목표를 위해 잠시 이 문제는 접어둔다" 라고 밝혀 두고 있다.
** 비유가 적절할지 모르겠으나, Alpha Go 등 요즈음의 artificial intelligence ( A.I.) 의 도약 발전과 관련해 잠시 비교를 해보자면... alpha go 는 19 by 19 격자 평면 공간 에서의 바둑게임에서 인간을 이겼다는 의미가 있을 지 모르겠으나, 리만가설은 무한대 by 무한대 격자 평면에서의 chaotic mapping ( 좀처럼 종 잡을 수 없는 mapping ) 을 다루는 문제라서 A. I. 도 1859년 리만이 남겼던 상기 언급과 비슷한 언급을....... 조만간(???) 하는 날이 오지 않을까 싶다.
( 2020. 02. 12. 김정건).
















서울대 김영훈 교수님의 "리만가설과 마이클 아티야" 란 글을 첨부한다. 학계에 계신 분의 글이기에 나같은 아마추어의 글과는 수준이 다르다.
건방진 소리지만, 리만가설을 조금이나마 이해 하는데 도움이 되는 정말 좋은 글이고 학자이시기 때문에 글의 정제된 표현이 정말 좋다.
(2020. 10. 08 첨부).
p.s. : 영문 번역본 page 5 의 첫번째와 두번째 식의 적분변수는 ds 가 아닌 dx 로 해야 옳다. 번역자의 실수.
'리만가설 개관' 카테고리의 다른 글
| RH 14 : 무한대의 실사리기 ζ ( s ) (0) | 2007.01.20 |
|---|---|
| RH 13 : 1859 리만논문 요약 (0) | 2007.01.20 |
| 사는 이야기 2 (0) | 2006.08.01 |
| RH 1 : 리만가설에 대한 나의 여행기 (0) | 2006.08.01 |
| RH 2 : 오일러 상수 (0) | 2006.08.01 |






































































