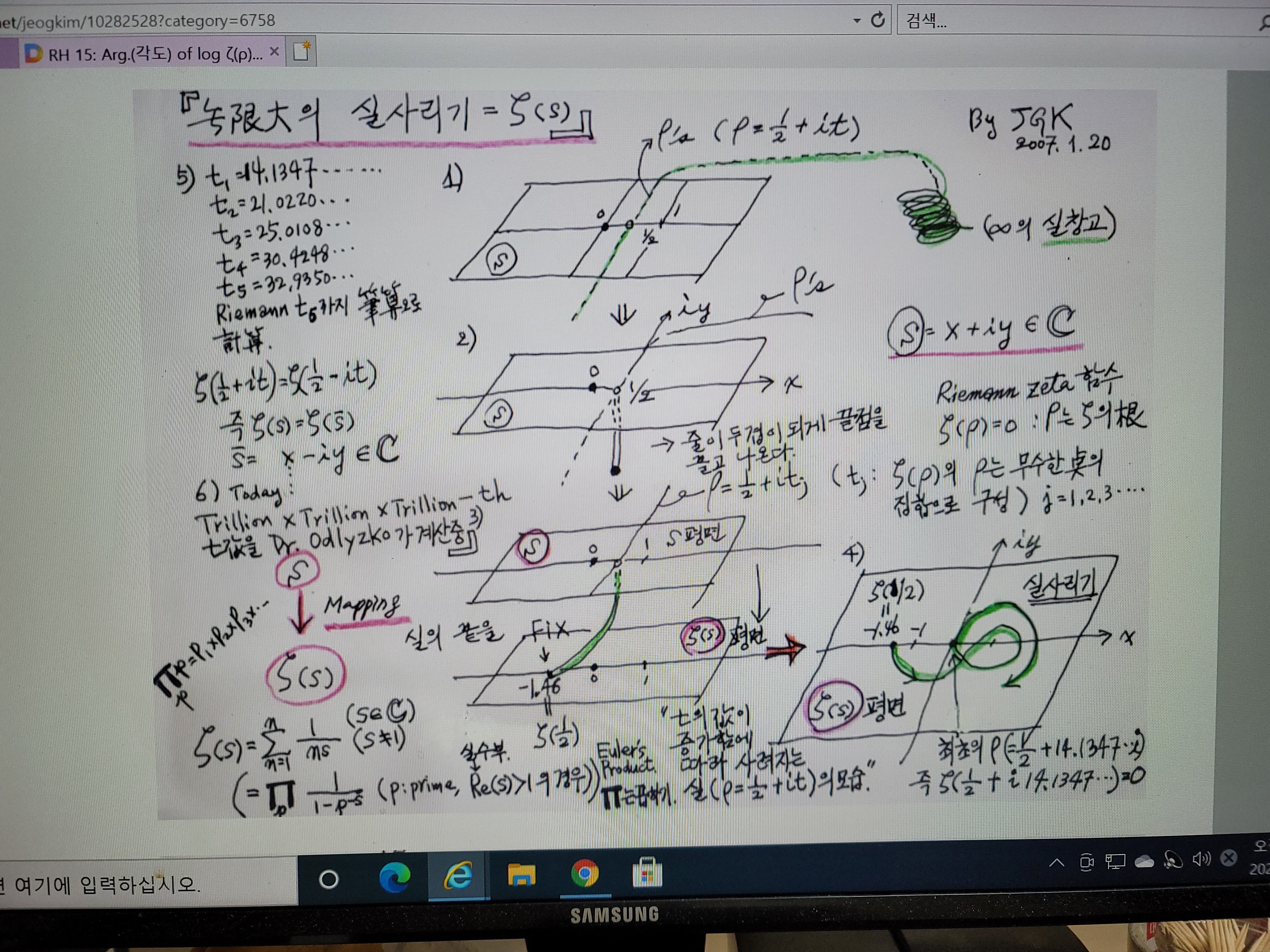


위에 올린 내 서툰 그림인 제타함수의 실(絲) 사리기는 http://math.ucsb.edu/~stopple/zeta.html
에 가면 칼라 그래픽화면을 볼수 있는데, 그 사이트의 화면상에 나오는 arg. of ζ(1/2 + it) 의 계산식
을 한번 필산으로 검토해 봤다. 글구, 실이 처음으로 고정되는 순간의 값 (-) 1.46은 1/2차원의
Unit Ball Volume(=1.46...) 이다.(나두 1/2 차원이 어떨지는 정말 모르겠으나 미분기하엔 그런 계산
공식이 있다).
제목의 예긴 뭔 예기냐 하면, 제타함수가 원점을 통과 할때는 각도값 ( Arg. of log ζ(ρ) ) 이
불연속치를 갖으며 ( 그값은 제타평면상의 원점(0)에 대응되는 s평면상의 각도값인데 원점에서 뭔
각도가 있겠는가?) 그것으로 제타함수의 근의 위치를 추정 할 수도 있다는 예기(그러나, 학문적으론
매우중요하다. 왜냐하면, s 평면으로 log ζ(ρ)가 들어올때는 discrete 한 불연속 직선이기 때문에 RH
를 푸는데 있어 중요한 고려점이 돼야한다.)
이글에선, 그게 중요한게 아니고, 제타함수가 원점을 치고 지나 갈때는 무한개의 모든(all) prime(소
수)들과 모든 자연수들이 동원되고, 작용을 하여(마치 무슨 신의 섭리같이) 그런 실 사리기의 궤적이
만들어 진다는 예기로서,
제타의 다른형태인 Euler Product 가 모든 prime 에 대한 곱이라는 사실의 반영이다. Euler Product
는 Re(s)>1 에 정의된 함수이다. (Michael Berry 같은 학자는 Primes의 음악을 들을수 있다했다,
실제로, 위에 소개한 사이트에 가면 소리를 들을 수 있는데 내 들어보니 소리는 별로였다).
평소,리만의 Analytic continuation 에 의한 ζ(s)(s=1 제외) 나 ξ(s)(entire function)의 경우에도
Euler Product가 유효하게 s평면 전체서 쓸 수 있느냐는게 나의 관심이었고, 그렇다라는게 나의
생각인데 영국물리학자 Sir Michael Berry의 생각도 비슷한거 같다. 이분에게, 나의 논문을 한번
보낸적이 있는데 친절하게 "한번 읽어는 보겠으나 검토는 못하겠다"고 회신을 해줘서 영국신사
의 manner를 느껴볼 수 있었고 읽어준 것만으로도 고맙다고 한적이 있었다.
그분은 H(classical hamiltonian)=xp 가 ζ(s)의 non-trivial zeros (ρ=1/2 + it)의 움직임을 관장하는
operator가 아니냐는 관점에서 Snaith란 학자와 연구하고 있다.그러니까 리만가설연구에 오래전 부터
물리학자들도 자기들의 관점에서 연구들을 해오고 있다는 사실이다.
David Hilbert 와 George Polya(지난번 하디의 일화를 소개할때 나왔던 그 사람이다)가 RH와 관련
해서, 제타함수의 근이 Hermitian Operator (당시 분들이 operator 라고 하는건 matrix 라고 한다,
당시는 Heisenberg나 Schroedinger의 양자역학이 정립되기 전으로 1910년대에 두 사람이 나눈예기)
와 연관이 있을거란 예기를 했었다는게, 그간 학계에 알려져 와서 그걸 많은이가 그걸 궁금해 했는데,
John Derbyshire의 책 Prime Obsession p.279에 보니 그건 공표된 얘긴 아니구( 독일교수들은
확실치 않은건 말로만하고 지나가는 모양이다, 그들의 권위때문에), 대신 Polya 가 Odlyzko 에게
보낸 편지사본이 있어 여기 원문을 인용해본다.
To : Andrew Odlyzko
(제타함수의 근을 수조개 이상씩 계속 구하고 있는 RH연구에 있어서의 실증적연구의 선두수학자)
This would be the case, I answered, if the non-trivial zeros of the ζ function were so
connected with the physical problem that the Riemann Hypothesis would be equivalent
to the fact that all the eigenvalues of the physical problem are REAL. I never published
the remarks, but somehow it became known and it is still remembered.
Yours Sincerely, George Polya.
단 한사람의 독자라도 있다면 본시리즈는 계속된다...
'리만가설 개관' 카테고리의 다른 글
| RH 17 : 새로써본 리만가설증명 - 나의 세번째 시도. (0) | 2007.02.12 |
|---|---|
| RH 16 : 최근 써본 Outlined Proof (0) | 2007.02.05 |
| RH 14 : 무한대의 실사리기 ζ ( s ) (0) | 2007.01.20 |
| RH 13 : 1859 리만논문 요약 (0) | 2007.01.20 |
| RH 12 : 리만가설 시리즈를 계속하며 (블로그 대표글) : 나름 공들여 작성한 문장, 자료와 수식들이 많습니다. (0) | 2007.01.16 |



